ICRA 2022
Learning Purely Tactile In-Hand Manipulation with a Torque-Controlled Hand
This site complements our ICRA 2022 paper Learning Purely Tactile In-Hand Manipulation with a Torque-Controlled Hand by Leon Sievers*, Johannes Pitz* and Berthold Bäuml.
Abstract
We show that a purely tactile dextrous in-hand manipulation task with continuous regrasping, requiring permanent force closure, can be learned from scratch and executed robustly on a torque-controlled humanoid robotic hand. The task is rotating a cube without dropping it, but in contrast to OpenAI’s seminal cube manipulation task, the palm faces downwards and no cameras but only the hand’s position and torque sensing are used. Although the task seems simple, it combines for the first time all the challenges in execution as well as learning that are important for using in-hand manipulation in real-world applications. We efficiently train in a precisely modeled and identified rigid body simulation with off-policy deep reinforcement learning, significantly sped up by a domain adapted curriculum, leading to a moderate 600 CPU hours of training time. The resulting policy is robustly transferred to the real humanoid DLR Hand-II, e.g., reaching more than 46 full 2π rotations of the cube in a single run and allowing for disturbances like different cube sizes, hand orientation, or pulling a finger.
Cite this paper as:
@inproceedings{Sievers2022,
author = {Leon Sievers and Johannes Pitz and Berthold B{\"a}uml},
booktitle = {Proc. IEEE International Conference on Robotics and Automation},
title = {Learning Purely Tactile In-Hand Manipulation with a Torque-Controlled Hand},
year = {2022}}
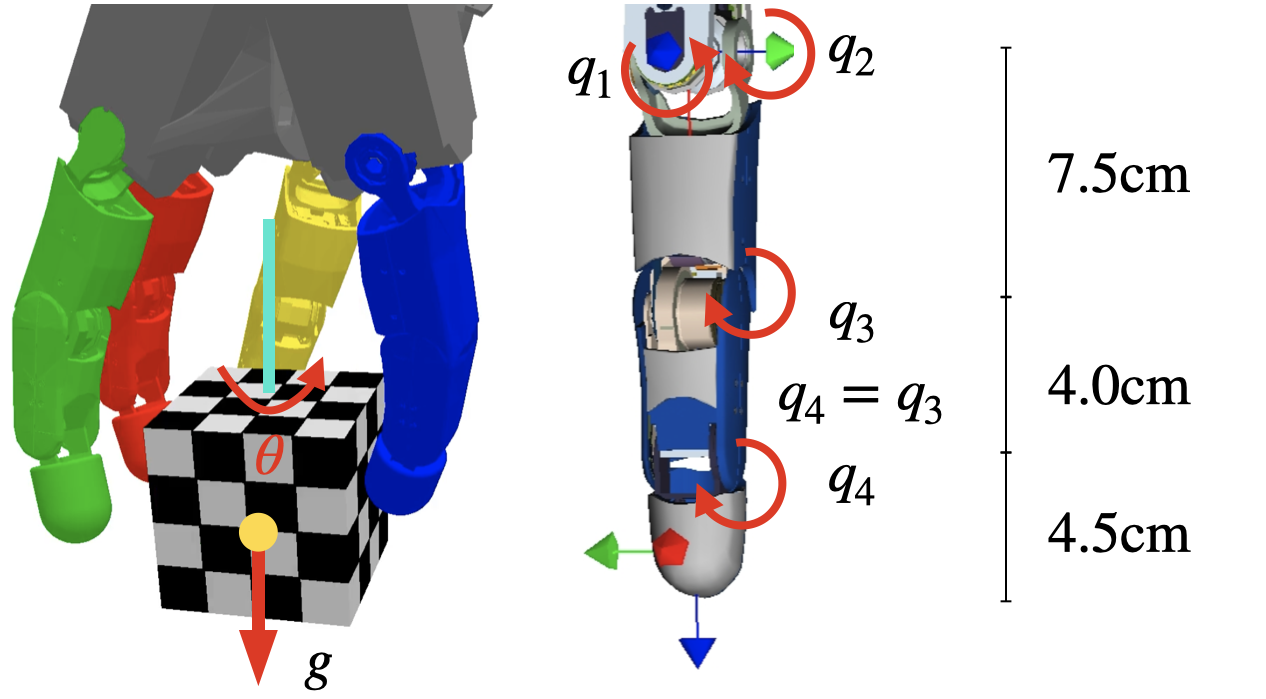
Hand
We use the DLR Hand II.
| \(q_1\) | \(q_2\) | \(q_3\) | |
| \(\Theta_{\text{min}}\) | \(-30^{\circ}\) | \(-20^{\circ}\) | \(-10^{\circ}\) |
| \(\Theta_{\text{max}}\) | \(30^{\circ}\) | \(86^{\circ}\) | \(105^{\circ}\) |
| \(\Theta_{\text{lower}}\) | \(-30^{\circ}\) | \(-10^{\circ}\) | \(-5^{\circ}\) |
| \(\Theta_{\text{upper}}\) | \(30^{\circ}\) | \(30^{\circ}\) | \(30^{\circ}\) |
| \(K_\text{P}\) | \(3.69 \frac{\text{Nm}}{\text{rad}}\) | \(3.69 \frac{\text{Nm}}{\text{rad}}\) | \(3.69 \frac{\text{Nm}}{\text{rad}}\) |
| \(K_\text{D}\) | \(0.25 \frac{\text{Nm s}}{\text{rad}}\) | \(0.25 \frac{\text{Nm s}}{\text{rad}}\) | \(0.25 \frac{\text{Nm s}}{\text{rad}}\) |
| \(K_\text{e}\) | \(25 \frac{\text{Nm}}{\text{rad}}\) | \(25 \frac{\text{Nm}}{\text{rad}}\) | \(25 \frac{\text{Nm}}{\text{rad}}\) |
| \(F_\text{static}\) | \(0.02\text{Nm}\) | \(0.02\text{Nm}\) | \(0.02\text{Nm}\) |
Hand dimensions as well as the angles and their limits. \(\Theta_{\text{min}}\) and \(\Theta_{\text{max}}\) denote the physical limits of the real kinematics while \(\Theta_{\text{lower}}\) and \(\Theta_{\text{upper}}\) are used for the simulated hand as well as the scaling of the network output. The PD Impedance Controller is parameterized by \(K_{\text{P}}\) and \(K_{\text{D}}\). The parasitic stiffness is modeled by \(K_{\text{e}}\). \(F_{\text{static}}\) denotes the static friction force.
Simulator
We are using PyBullet as our rigid body simulator.
Simulator Configuration
Initial Learning
| earth_acceleration | 9.81 \(\frac{\text{m}}{\text{s}^2}\) |
| simulation_frequency | 500 \(\text{Hz}\) |
| network_frequency | 10 \(\text{Hz}\) |
| steps_before_gravity_onset | 4 |
| friction_lateral_tip | 0.9 |
| friction_lateral_others | 0.09 |
| friction_lateral_tip_random | 0.0 |
| friction_spinning | 0.1 |
| cube_mass | 0.05 \(\text{kg}\) |
| cube_length | 0.08 \(\text{m}\) |
| cube_mass_random | 0.005 \(\text{kg}\) |
| cube_position_random | [0.001, 0.001, 0.005] \(\text{m}\) |
| cube_rotation_random | [0.01, 0.01, 0.1] \(\text{rad}\) |
| motor_noise_std | 0.002 \(\text{rad}\) |
| sticky_action_probability | 0.1 |
Continue Learning
| friction_lateral_tip_random | 0.1 |
| friction_spinning | 0.1 |
| motor_noise_std | 0.02 \(\text{rad}\) |
Learning
We use the Soft Actor-Critic Algorithm.
Reward Constants
| \(\lambda_{\text{spin}}\) | 16 |
| \(\lambda_{\text{Z}}\) | 100 |
| \(\lambda_{\text{plane}}\) | 300 |
| \(\lambda_{\text{rot}}\) | 50 |
| \(\lambda_{\text{proxy}}\) | 25 |
Learning Configuration
Initial Learning
| num_worker | 12 |
| local_steps_per_update | 25 |
| gradient_steps_per_update | 100 |
| batch_size | 256 |
| initial_no_update | 2000 |
| initial_random_steps | 10000 |
| curriculum_start | 2e6 |
| curriculum_length | 4e6 |
| num_layers | 2 |
| hidden_size | 512 |
| replay_size | 1.5e5 |
| entropy_target | -6 |
| alpha_initial | 0.2 |
| gamma | 0.9 |
| lambda_weight_decay | 2.5e-4 |
| max_episode_length | 100 |
| num_observation_stack | 5 |
| max_reward_rotation | 1 \(\frac{\text{rad}}{\text{s}}\) |
Continue Learning
| replay_size | 1.5e6 |
| entropy_target | -8 |
| gamma | 0.92 |
| lambda_weight_decay | 2.5e-4 |
| max_episode_length | 200 |
| num_observation_stack | 5 |
| max_reward_rotation | 0.7 \(\frac{\text{rad}}{\text{s}}\) |