IROS 2024
Fine Manipulation Using a Tactile Skin: Learning in Simulation and Sim-to-Real Transfer
This site complements our paper Fine Manipulation Using a Tactile Skin: Learning in Simulation and Sim-to-Real Transfer by Ulf Kasolowsky and Berthold Bäuml accepted for the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems.
Abstract
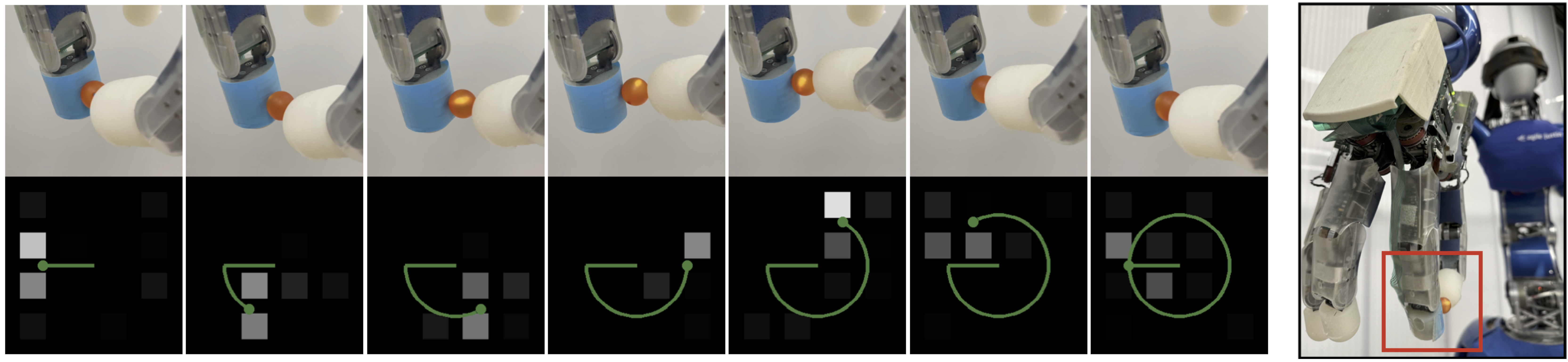
We want to enable fine manipulation with a multi-fingered robotic hand by using modern deep reinforcement learning methods. Key for fine manipulation is a spatially resolved tactile sensor. Here, we present a novel model of a tactile skin that can be used together with rigid-body (hence fast) physics simulators. The model considers the softness of the real fingertips such that a contact can spread across multiple taxels of the sensor depending on the contact geometry. We calibrate the model parameters to allow for an accurate simulation of the real-world sensor. For this, we present a self-contained calibration method without external tools or sensors. To demonstrate the validity of our approach, we learn two challenging fine manipulation tasks: Rolling a marble and a bolt between two fingers. We show in simulation experiments that tactile feedback is crucial for precise manipulation and reaching sub-taxel resolution of < 1 mm (despite a taxel spacing of 4 mm). Moreover, we demonstrate that all policies successfully transfer from the simulation to the real robotic hand.
Cite this paper as:
@inproceedings{kasolowsky2024,
author = {Ulf Kasolowsky and Berthold B{\"a}uml},
booktitle = {IEEE International Conference on Intelligent Robots and Systems},
title = {Fine Manipulation Using a Tactile Skin: Learning in Simulation and Sim-to-Real Transfer},
year = {2024}
}
Domain Randomization
We distinguish two types of domain randomization: Inter-episode and intra-episode randomizations. The first type refers to parameters sampled at the beginning of an episode and then kept constant. The latter is sampled periodically throughout an episode. While \(N(\mu, \sigma)\) denotes a normal distribution with mean \(\mu\) and standard deviation \(\sigma\), \(U(a, b)\) and \(LogU(a, b)\) denote a uniform and log-uniform distribution in the range from \(a\) to \(b\), respectively.
Finger Parameters
| Parameter | Unit | Type | Distribution | |
|---|---|---|---|---|
| Joint offsets | $$q_\text{off}$$ | $$\text{rad}$$ | inter | $$U(-0.04, 0.04)$$ |
| Joint noise | $$q_\text{noise}$$ | $$\text{rad}$$ | intra | $$N(0.0, 0.02)$$ |
| Proportional gain | $$K_p$$ | $$\text{N}\,\text{m}\,\text{rad}^{-1}$$ | inter | $$U(4.8, 5.2)$$ |
| Damping gain | $$K_d$$ | $$\text{N}\,\text{m}\,\text{s}\,\text{rad}^{-1}$$ | inter | $$U(0.26, 0.33)$$ |
| Parasitic stiffness | $$K_e$$ | $$\text{N}\,\text{m}\,\text{rad}^{-1}$$ | inter | $$U(15, 35)$$ |
| Stick friction | $$\mu_{\text{stick},1/2}$$ | $$\text{N}\,\text{m}$$ | inter | $$U(0.01, 0.03)$$ |
| $$\mu_{\text{stick},3}$$ | $$\text{N}\,\text{m}$$ | inter | $$U(0.07, 0.09)$$ | |
Object Parameters
| Parameter | Unit | Type | Distribution | ||
|---|---|---|---|---|---|
| Marble | Bolt | ||||
| Position offset | $$\Delta x$$ | $$\text{mm}$$ | inter | $$U(-2.0, 2.0)$$ | |
| Orientation offset | $$\psi$$ | $$^\circ$$ | inter | n. a. | $$U(-5, 5)$$ |
| $$\theta$$ | $$^\circ$$ | inter | n. a. | $$U(-5, 5)$$ | |
| $$\phi$$ | $$^\circ$$ | inter | n. a. | $$0.0$$ | |
| Mass | $$m$$ | $$\text{g}$$ | inter | $$U(3.0, 5.0)$$ | $$U(5.0, 7.0)$$ |
| Radius | $$R$$ | $$\text{mm}$$ | inter | $$U(4.0, 8.0)$$ | $$6.0$$ |
| Lateral friction | $$\mu_\text{lat}$$ | $$1$$ | inter | $$U(1.1, 1.3)$$ | $$U(0.8, 1.0)$$ |
| Spinning friction | $$\mu_\text{spin}$$ | $$1$$ | inter | $$LogU(2\times10^{-3}, 2\times10^{-2})$$ | |
| Random forces | $$F_\text{rand}$$ | $$N$$ | intra | $$U(-4\times10^{-3}, 4\times10^{-3})$$ | |
Skin Parameters
| Parameter | Unit | Type | Distribution | |
|---|---|---|---|---|
| Sensor position | $$y$$ | $$\text{mm}$$ | inter | $$U(21.5, 25.5)$$ |
| $$\beta$$ | $$^\circ$$ | inter | $$U(-12, 12)$$ | |
| $$\alpha$$ | $$^\circ$$ | inter | $$U(-15, 15)$$ | |
| Elasticity | $$E$$ | $$\text{MPa}\,\text{m}^{-1}$$ | inter | $$U(236, 848)$$ |
| Scale | $$S_j$$ | $$\text{N}^{-1}$$ | inter | $$U(61, 76)$$ |
| Taxel offsets | $$T_\text{off}$$ | $$1$$ | inter | $$U(-5, 5)$$ |
| Noise range | $$\sigma_\text{taxel}$$ | $$1$$ | inter | $$U(0, 5)$$ |
| Taxel noise | $$T_\text{noise}$$ | $$1$$ | intra | $$N(0, \sigma_\text{noise})$$ |
Learning Configuration
To train the policies, we relied on the Soft-Actor-Critic algorithm (SAC).
Learning Parameters
| Parameter | Value |
|---|---|
| Number of environments | $$8$$ |
| Replay buffer sixe | $$2 \times 10^5$$ |
| Steps before learning | $$6000$$ |
| Training interval | $$60\,\text{steps}$$ |
| Gradient steps | $$200$$ |
| Discount factor | $$0.95$$ |
| Polyak update | $$5\times 10^{-3}$$ |
| Target entropy | $$-4.0$$ |
| Initial entropy coefficient | $$0.2$$ |
| Learning rate | $$3\times 10^{-4}$$ |
| Batch size | $$256$$ |
Reward Constants
| $$\lambda_p$$ | $$\lambda_g$$ | $$\lambda_f$$ | $$\lambda_\alpha$$ | $$\lambda_q$$ | $$\lambda_\dot{q}$$ | $$\lambda_\tau$$ | |
|---|---|---|---|---|---|---|---|
| Marble | $$0.15$$ | $$0.05$$ | $$0.05$$ | n. a. | $$0.01$$ | $$0.01$$ | $$0.01$$ |
| Bolt | $$0.15$$ | $$0.05$$ | $$0.05$$ | $$0.05$$ | $$0.01$$ | $$0.01$$ | $$0.01$$ |