OMP
We used our own variant of CHOMP as optimization-based solver to generate the dataset and post-process the predictions of the neural network. The main difference is that we dynamically add sub steps to ensure no collisions are missed when discretizing the path
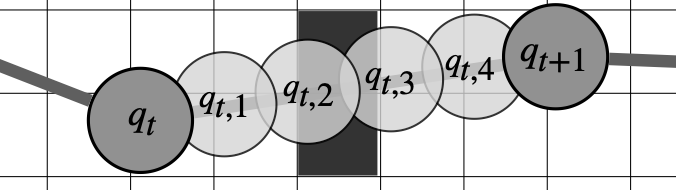Substeps between two discrete waypoints \(q_t\) and \(q_{t+1}\) to explicitly calculate the swept volume of the path and ensure no obstacles are missed.
Path
\[Q = [q_1, \dots, q_{\mathrm{t}}], \, q_t \in \mathbb{R}^{N_{\mathrm{q}}}\]Objective Function
\[U(Q) = U_c(Q) + \alpha \, U_s(Q) + \beta \, U_l(Q)\]Length Cost
\[U_l(Q) = \frac{N_{\mathrm{t}}-1}{|q_{N_{\mathrm{t}}}-q_1|^2} \sum_{t=1}^{N_{\mathrm{t}}-1} |q_{t+1} - q_{t}|^2\]Collision Cost
\[U_c(Q) = \sum_{t, r}^{N_{\mathrm{t}}, N_{\mathrm{r}}} \sum_{i=1}^{N_{\mathrm{f}}} \sum_{k=1}^{N_{\mathrm{s}}} c \Big( D \big( F_i(q_{t, r}) \cdot{} x_{ik} \big) - r_{ik} \Big)\]Smooth Clipping Function
\[\begin{aligned} c(d) &= \left\{ \begin{array}{ll} -d + \frac{\epsilon}{2} & \text{, if } d < 0 \\ \frac{1}{2 \epsilon} (d - \epsilon)^2 & \text{, if } 0 \leq d \leq \epsilon \\ 0 & \text{, if } \epsilon < d \end{array} \right. \end{aligned}\]Self-collision Cost
\[U_s(Q) = \sum_{t, r}^{N_{\mathrm{t}}, N_{\mathrm{r}}} \, \sum_{j>i}^{N_{\mathrm{f}}, N_{\mathrm{f}}} \, \sum_{k, l}^{N_{\mathrm{s}i}, N_{\mathrm{s}j}} c \big( \big| F_{i}(q_{t, r}) \cdot x_{ik} - F_{j}(q_{t, r}) \cdot x_{jl} \big| - r_{ik} - r_{jl} \big)\]